四棱錐的面相是什么樣的 4棱錐圖片
四棱錐是一種常見(jiàn)的多面體,由一個(gè)四邊形底面和四個(gè)三角形側面組成。了解四棱錐的面相有助于更好地理解其幾何特性和應用場(chǎng)景。
底面
四棱錐的底面是一個(gè)四邊形,可以是正方形、矩形或其他四邊形。正四棱錐的底面是正方形,四條邊長(cháng)度相等。底面的形狀決定了四棱錐的基本幾何特性,正方形底面使得四棱錐的對稱(chēng)性和穩定性更好。
側面
四棱錐的側面是四個(gè)全等的等腰三角形,這些三角形有一個(gè)公共頂點(diǎn),即四棱錐的頂點(diǎn)。每個(gè)等腰三角形的底邊等于底面四邊形的邊長(cháng)。側面是全等的等腰三角形,確保了四棱錐的對稱(chēng)性和均勻性,同時(shí)也使得四棱錐的幾何特性更加明確。
頂點(diǎn)
四棱錐的頂點(diǎn)是四個(gè)側面的公共頂點(diǎn),位于底面的中心垂直上方。頂點(diǎn)是四棱錐的高和斜高的交點(diǎn),決定了四棱錐的高度和傾斜程度。
分瓣形展開(kāi)圖
四棱錐的展開(kāi)圖可以是分瓣形,底面不剪開(kāi),將每個(gè)側面依次展開(kāi)。這種展開(kāi)圖有助于理解四棱錐的側面結構和連接方式。分瓣形展開(kāi)圖直觀(guān)地展示了四棱錐的側面展開(kāi)后的形狀,有助于理解其三維結構。
扇子拖尾巴型展開(kāi)圖
另一種展開(kāi)圖是扇子拖尾巴型,底面剪開(kāi)一條棱,側面整體展開(kāi)。這種展開(kāi)圖展示了四棱錐底面的完整形狀和側面的展開(kāi)狀態(tài)。扇子拖尾巴型展開(kāi)圖不僅展示了四棱錐的側面結構,還清晰地顯示了底面的形狀,有助于全面理解四棱錐的結構。
建筑和工程
四棱錐在建筑和工程中有廣泛應用,特別是在需要高穩定性和承載能力的結構中。例如,金字塔和許多古代建筑中的塔樓都采用了四棱錐的形狀。四棱錐的形狀因其穩定性和美觀(guān)性而被廣泛應用,特別是在需要承載重量的結構中。
雕塑和藝術(shù)
四棱錐的形狀也被廣泛應用于雕塑和藝術(shù)作品中,藝術(shù)家通過(guò)四棱錐表達復雜的空間結構和光影效果。四棱錐的幾何形狀和空間特性使其成為藝術(shù)家表達復雜情感和概念的重要工具。
體積和表面積公式
正四棱錐的體積公式為 \\( V = \\frac{1}{3}Sh \\),其中 \\( S \\) 是底面積,\\( h \\) 是高。表面積公式為 \\( S = s(4h^2 + s^2) \\),其中 \\( s \\) 是底面邊長(cháng)。
這些公式是計算四棱錐體積和表面積的基礎,理解這些公式有助于在實(shí)際應用中進(jìn)行準確的計算和設計。
四棱錐由一個(gè)四邊形底面和四個(gè)全等的等腰三角形側面組成,頂點(diǎn)位于底面的中心垂直上方。其展開(kāi)圖可以是分瓣形或扇子拖尾巴型,展示了四棱錐的不同側面結構。四棱錐在建筑和工程中有廣泛應用,也常用于雕塑和藝術(shù)作品中。理解四棱錐的幾何特性和數學(xué)公式有助于更好地應用和欣賞這種幾何形狀。
四棱錐的底面是一個(gè)四邊形。根據具體類(lèi)型,底面可以是正方形、矩形、菱形或其他四邊形。例如,正四棱錐的底面是正方形,而一般四棱錐的底面可以是任意四邊形。
四棱錐的側面是四個(gè)三角形。
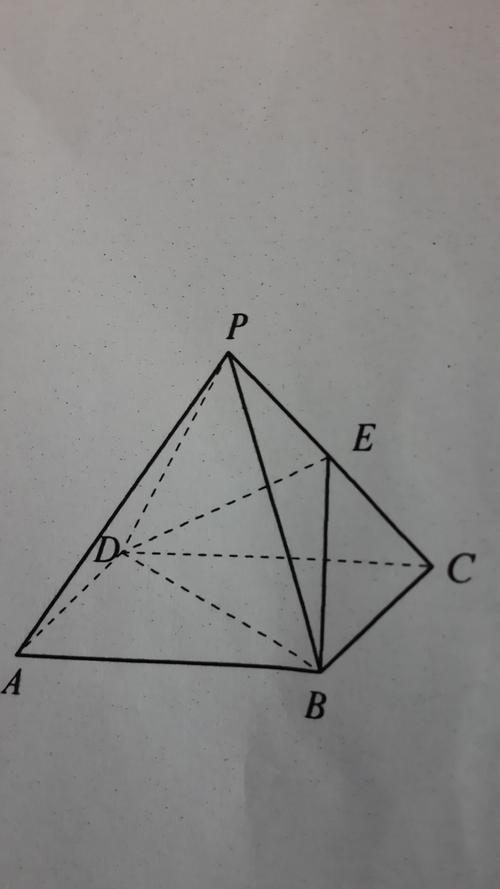
四棱錐的頂點(diǎn)與底面的關(guān)系是幾何學(xué)中一個(gè)重要的概念,尤其在繪畫(huà)和幾何學(xué)中有著(zhù)廣泛的應用。以下是關(guān)于四棱錐頂點(diǎn)與底面關(guān)系的詳細解釋?zhuān)?/p>
定義
四棱錐:底面為四邊形,側面為四個(gè)三角形的立體幾何體。正四棱錐特指底面為正方形的四棱錐。
頂點(diǎn):四棱錐的頂部,所有側面的公共頂點(diǎn)。
底面:四棱錐的底部,通常為四邊形,正四棱錐的底面為正方形。
關(guān)系
頂點(diǎn)在底面的投影:正四棱錐的頂點(diǎn)在底面的投影是底面的中心,即正方形的中心。
側面與底面的關(guān)系:正四棱錐的側面是四個(gè)全等的等腰三角形,每個(gè)三角形的底邊是底面正方形的邊。
性質(zhì)
等腰三角形:正四棱錐的各側面都是全等的等腰三角形,斜高相等。
直角三角形:正四棱錐的高、斜高和斜高在底面內的射影組成一個(gè)直角三角形。
角度相等:正四棱錐的側棱與底面所成的角都相等,側面與底面所成的二面角也相等。
體積與表面積
體積公式:正四棱錐的體積公式為 $V = \\frac{1}{3} \
imes S \
imes h$,其中 $S$ 為底面積,$h$ 為高。
表面積公式:正四棱錐的表面積公式為 $S_{\
ext{表面積}} = 4S_{\
riangle PAB} + S_{\
ext{底}}$,其中 $S_{\
riangle PAB}$ 為側面三角形的面積,$S_{\
ext{底}}$ 為底面積。